# 一文搞懂:因数、质数、质因数(超详细通俗版)
*数学知识*
一篇**通俗易懂、图文结合风格**的文章,带你彻底搞懂“因数”“质数”“质因数”这三个数学中的基础但重要的概念
## 目录
[TOC]
---
# 🌟 一文搞懂:因数、质数、质因数(超详细通俗版)
你有没有遇到过这样的问题:
> “10000 以内,有多少个数和 10000 互质?”
> “这个数的质因数有哪些?”
> “什么是质数?”
别担心,这篇文章就用最生活化的方式,带你从零开始理解这些概念。
我们先从一个最基础的问题说起:
---
## 🔹 什么是“因数”?
### ✅ 定义:
**如果一个数能被另一个数整除(没有余数),那么这个“另一个数”就是它的因数。**
比如:
6 ÷ 2 = 3(刚好除尽)→ 所以 **2 是 6 的因数**
6 ÷ 3 = 2 → 所以 **3 也是 6 的因数**
6 ÷ 4 = 1.5(有小数)→ 所以 4 不是 6 的因数
---
### ✅ 举个生活例子:
想象你有 **6 块巧克力**,要平均分给一些小朋友,每人分得整块(不能切开),你能怎么分?
- 分给 1 个人:每人 6 块 ✅
- 分给 2 个人:每人 3 块 ✅
- 分给 3 个人:每人 2 块 ✅
- 分给 4 个人:每人 1 块,剩 2 块 ❌(不整除)
- 分给 6 个人:每人 1 块 ✅
所以,能平均分的“人数”是:1, 2, 3, 6
👉 这些就是 **6 的因数**
---
### ✅ 小结:
> **因数 = 能整除这个数的数**
6 的所有因数是:**1, 2, 3, 6**
---
## 🔹 什么是“质数”?(也叫“素数”)
### ✅ 定义:
**只有两个因数的数,就是质数:1 和它自己。**
也就是说,**除了 1 和它本身,再没有别的因数了。**
---
### ✅ 举几个例子:
| 数字 | 因数有哪些? | 是质数吗? | 说明 |
|------|---------------|-------------|------|
| 2 | 1, 2 | ✅ 是 | 最小的质数,唯一的偶数质数 |
| 3 | 1, 3 | ✅ 是 | 不能被 2 整除 |
| 4 | 1, 2, 4 | ❌ 否 | 有三个因数(多了 2) |
| 5 | 1, 5 | ✅ 是 | 只能被 1 和 5 整除 |
| 6 | 1, 2, 3, 6 | ❌ 否 | 因数太多 |
| 7 | 1, 7 | ✅ 是 | 是质数 |
| 9 | 1, 3, 9 | ❌ 否 | 能被 3 整除 |
---
### ✅ 生活比喻:
质数就像“不可再分的积木块”。
比如你有一堆乐高,有些是“单块”的(比如 2、3、5、7),它们不能再拆成更小的整数组合 → 这些就是**质数**。
而像 6、8、9 这样的数,可以“拆开”,它们是“组合块” → 这些叫**合数**。
---
### ✅ 常见质数表(记住前几个很有用):
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47…
> 📌 **记住:1 不是质数!**
> 因为它只有一个因数(就是 1),不符合“两个因数”的要求。
---
## 🔹 什么是“质因数”?
### ✅ 定义:
**既是因数,又是质数的数,就叫质因数。**
---
### ✅ 例子:找 12 的质因数
先找 12 的所有因数:
1, 2, 3, 4, 6, 12
再从中挑出“质数”:
- 1 → ❌(不是质数)
- 2 → ✅ 是质数
- 3 → ✅ 是质数
- 4 → ❌(4=2×2,不是质数)
- 6 → ❌(6=2×3,不是质数)
- 12 → ❌(合数)
所以,12 的质因数是:**2 和 3**
---
### ✅ 更进一步:质因数分解
我们不仅要知道“有哪些质因数”,还想把原数“拆成质数相乘”的形式。
这就是**质因数分解**。
#### 例子:分解 12
```
12 ÷ 2 = 6 → 记下 2
6 ÷ 2 = 3 → 再记一个 2
3 ÷ 3 = 1 → 记下 3
```
所以:
$$
12 = 2 × 2 × 3 = 2^2 × 3
$$
✅ 分解完成!
---
### ✅ 再来一个大一点的:100
```
100 ÷ 2 = 50 → 2
50 ÷ 2 = 25 → 2
25 ÷ 5 = 5 → 5
5 ÷ 5 = 1 → 5
```
所以:
$$
100 = 2 × 2 × 5 × 5 = 2^2 × 5^2
$$
---
## 🔹 为什么质因数这么重要?
### ✅ 因为它是“数的基因”!
就像人有 DNA 一样,每个数也有它的“数字基因”——就是它的质因数。
一旦你知道了一个数的质因数分解,你就能:
- 快速求最大公约数(GCD)
- 快速求最小公倍数(LCM)
- 判断它有多少个因数
- 计算欧拉函数(用于密码学、竞赛题)
- 解决“互质”类问题
---
### ✅ 举个例子:求 100 的因数个数
我们知道:
$$
100 = 2^2 × 5^2
$$
求因数个数的公式是:
> 每个质因数的指数 +1,然后相乘
所以:
$$
(2+1) × (2+1) = 3 × 3 = 9
$$
✅ 100 有 9 个因数:1, 2, 4, 5, 10, 20, 25, 50, 100
---
## 🔹 如何判断一个数是不是质数?
### ✅ 方法:试除法
要判断一个数 $ n $ 是不是质数,只需要试除 **小于等于 $ \sqrt{n} $** 的所有质数。
#### 例子:判断 29 是不是质数
√29 ≈ 5.4,所以我们只需要试除到 5:
- 能被 2 整除吗?29 是奇数 → ❌
- 能被 3 整除吗?2+9=11,不能被 3 整除 → ❌
- 能被 5 整除吗?末位不是 0 或 5 → ❌
→ 没有因数,所以 **29 是质数!✅**
---
## 🔹 小技巧:快速判断能否被小质数整除
| 质数 | 判断方法 |
|------|----------|
| **2** | 末位是偶数(0,2,4,6,8) |
| **3** | 各位数字之和能被 3 整除 |
| **5** | 末位是 0 或 5 |
| **11** | 奇数位和 - 偶数位和 能被 11 整除(如 121:1+1 - 2 = 0) |
---
## 🔹 总结:一张表搞定所有概念
| 概念 | 定义 | 例子(以 12 为例) |
|------|------|------------------|
| **因数** | 能整除这个数的数 | 1, 2, 3, 4, 6, 12 |
| **质数** | 只有 1 和它本身两个因数的数 | 2, 3, 5, 7, 11… |
| **质因数** | 既是因数又是质数的数 | 2, 3 |
| **质因数分解** | 把数写成质数相乘的形式 | $ 12 = 2^2 × 3 $ |
---
## ✅ 一句话总结:
> **每个合数都可以唯一地分解成若干个质数的乘积,这些质数就是它的“质因数”——它们是构成所有数字的“基本积木”。**
---
## 🎯 练习时间(动手试试看!)
1. 找出 18 的所有因数
2. 判断 17 是不是质数
3. 把 60 分解成质因数
4. 100 以内有多少个质数?(提示:可以查质数表)
💡 答案:
1, 2, 3, 6, 9, 18
是质数(只能被 1 和 17 整除) .
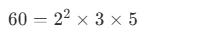
共 25 个(2, 3, 5, 7, 11, ..., 97)
---
📌 **记住:数学不是死记硬背,而是理解+练习。**
只要你掌握了“因数、质数、质因数”,后面学最大公约数、欧拉函数、互质问题都会变得非常简单!
------
***操作记录***
作者:[zhao](https://www.lingyuzhao.top//index.html?search=4 "zhao")
操作时间:2025-08-03 20:22:43 星期日 【时区:UTC 8】
事件描述备注:保存/发布
中国 天津市 天津
[](如果不需要此记录可以手动删除,每次保存都会自动的追加记录)
