# 概率计算:通俗易懂的全面指南 *数学知识* 概率是数学中一个非常有趣且实用的领域,它帮助我们理解和预测事件发生的可能性。无论你是学生、专业人士还是对概率感兴趣的任何人,本文都将带你深入了解概率的基本概念以及如何在不同条件下计算概率。 ## 目录 [TOC] 当然可以!以下是一个整合版的内容,包含了之前关于概率计算的通俗易懂介绍以及条件概率的具体计算方法。为了满足你的要求,去除了排列组合部分,并确保内容全面且易于理解。 --- ### 概率计算:通俗易懂的全面指南 概率是数学中一个非常有趣且实用的领域,它帮助我们理解和预测事件发生的可能性。无论你是学生、专业人士还是对概率感兴趣的任何人,本文都将带你深入了解概率的基本概念以及如何在不同条件下计算概率。 #### 什么是概率? 概率是用来度量某个事件发生的机会大小的一个数值,范围从0到1。如果一个事件的概率为0,表示该事件不可能发生;如果概率为1,则意味着这个事件肯定会发生。介于两者之间的值表示事件发生的可能性程度。 #### 基本概率计算 假设你有一个装有5个红球和3个蓝球的袋子,问从中随机取出一个球是红色的概率是多少? - **总可能结果数** = 红球数 + 蓝球数 = 5 + 3 = 8 - **有利结果数(取到红球)** = 5 - 因此,取到红球的概率 = 5/8 #### 条件概率 条件概率是指在已知某一事件发生的前提下,另一事件发生的概率。例如,在上述例子中,如果我们已经知道取出的是一个红球,那么接下来再取出一个红球的概率是多少? 这里需要用到条件概率公式: 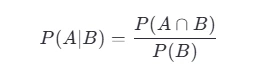 其中,`P(A|B)` 表示在B发生的条件下A发生的概率,`P(A n B)` 是A和B同时发生的概率,而 `P(B)` 是B发生的概率。 继续上面的例子,第一次取出红球后不放回,第二次再取一个红球的概率变为: - **新的总可能结果数** = 7(因为第一次已经取出了一个红球) - **新的有利结果数(取到红球)** = 4 - 因此,第二次取到红球的概率 = 4/7 ##### 示例问题:求第二次取到红球的概率,已知第一次取到了红球。 1. **定义事件**: - 事件 \(A\):第二次取到红球。 - 事件 \(B\):第一次取到红球。 2. **计算 \(P(B)\)**: - 第一次取到红球的概率 \(P(B) = 5/8 (因为总共有5个红球,共8个球)。 3. **计算 \(P(A n B)\)**: - 这里 \(P(A n B)\) 实际上是指第一次和第二次都取到红球的概率。 - 第一次取到红球的概率是 5/8。 - 在第一次已经取到一个红球后,袋子里剩下4个红球和3个蓝球,总共7个球。因此,第二次再取到红球的概率变为4/7。 - 因此,\(P(A n B)\) 即两次连续取到红球的概率为 P(A) × p(B) = (5/8) × (4/7) = 5/14 4. **使用条件概率公式计算 \(P(A|B)\)**: 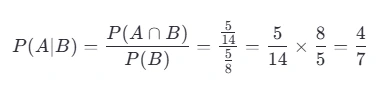 所以,在已知第一次取到红球的情况下,第二次取到红球的概率是 4/7 ### 理解联合概率 \(P(A n B)\) 联合概率 \(P(A n B)\) 表示事件 \(A\) 和 \(B\) 同时发生的概率。对于独立事件,我们可以简单地将它们各自的概率相乘: 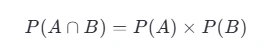 但是,在我们的例子中,事件 \(A\) 和 \(B\) 并不是独立的(因为第一次取球的结果影响了第二次取球的概率)。因此,我们需要按照实际情况来计算联合概率。 ### 另一个例子:独立事件 假设我们有两个独立事件: - 事件 \(A\):抛一枚公平硬币得到正面。 - 事件 \(B\):掷一颗六面骰子得到点数为6。 在这种情况下: - \(P(A) = 1/2 - \(P(B) = 1/6 由于这两个事件是独立的,联合概率 \(P(A n B)\) 就是各自概率的乘积: 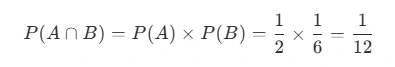 如果我们想知道在事件 \(B\) 发生的情况下事件 \(A\) 发生的概率,即 \(P(A|B)\),由于事件 \(A\) 和 \(B\) 是独立的,我们知道: 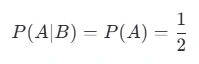 这符合直觉,因为抛硬币的结果不应该受到掷骰子结果的影响。 ### 独立与非独立事件 两个事件是独立的,如果其中一个事件的发生不影响另一个事件的发生概率。比如抛硬币两次,每次出现正面的概率都是0.5,这两次抛掷是独立事件。 对于独立事件,联合概率可以简单地通过乘法原则来计算: 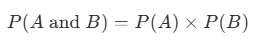 然而,如果事件不是独立的(如上例中的连续取球),我们需要使用条件概率的概念来进行计算。 ### 总结 - **概率**是用来度量某个事件发生的机会大小的一个数值,范围从0到1。 - **条件概率 \(P(A|B)\)** 表示在事件 \(B\) 发生的条件下事件 \(A\) 发生的概率,计算公式为 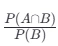 - **联合概率 \(P(A \cap B)\)** 是事件 \(A\) 和 \(B\) 同时发生的概率。如果 \(A\) 和 \(B\) 是独立事件,则 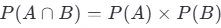 ;否则,需要根据具体情况计算。 - 在实际应用中,理解事件是否独立非常重要,因为它会影响联合概率的计算方式。 希望这些解释和例子能够帮助你更好地理解概率的基础知识及其在不同条件下的应用!如果有任何进一步的问题或需要更多例子,请随时告诉我。 ------ ***操作记录*** 作者:[zhao](https://www.lingyuzhao.top//index.html?search=4 "zhao") 操作时间:2025-08-05 20:17:19 星期二 【时区:UTC 8】 事件描述备注:保存/发布 中国 天津市 天津 [](如果不需要此记录可以手动删除,每次保存都会自动的追加记录)
