# 2018 全国青少年信息学奥林匹克联赛初赛(普及组)试题解析 - 选择部分
*信奥赛*
2018 全国青少年信息学奥林匹克联赛初赛(普及组)试题解析 含题目
## 目录
[TOC]
## 一 选择题
### 1,以下属于输出设备的是( )。
A. 扫描仪
B. 键盘
C. 鼠标
D. 打印机
>解析:D
----
### 2,下列4个不同进制的数中,与其他3项数值不相等的是( )。
A. (269)₁₆
B. (617)₁₀
C. (1151)₈
D. (1001101011)₂
> 解析:根据 https://www.lingyuzhao.top/b/Article/-5001662716451593 文章可以查看到计算方法
> 0x269 = 256x2+16x6+9x1 = 512+96+9 = 617
> 其中 256 16 是位权,9×16^0 = 9x1
> 617 就是 10进制 不需要计算
> 01151 = 512x1+64x1+8x5+1= 512+64+40+1 = 512+105 = 617
> 到这里就不需要算了 答案已经出现了 D 是不一样的 A 都是一样的
----
### 3,1MB等于( )。
A. 1000字节
B. 1024字节
C. 1000×1000字节
D. 1024×1024字节
> 1024 的单位汇率
> 1MB = 1024x1KB
> 1KB = 1024x1B
> 因此 1MB = 1024x1024 字节 选择D
----
### 4,广域网的英文缩写是( )。
A. LAN
B. WAN
C. MAN
D. LNA
> 全拼是 Wide area network 缩写是 WAN
----
### 5,中国计算机学会于( )年创办全国青少年计算机程序设计竞赛。
A. 1983
B. 1984
C. 1985
D. 1986
> 宗教题目 直接选 B
----
### 6,如果开始时计算机处于小写输入状态,现在有一只小老鼠反复按照 Caps Lock、字母键 A、字母键 S、字母键 D、字母键 F 的顺序循环按键,即 Caps Lock、A、S、D、F、Caps Lock、A、S、D、F……,屏幕上输出的第 81 个字符是字母( )。
A. A
B. S
C. D
D. a
> 首先要注意是屏幕哦~ A S D F 会出现 这里是个小误区
> 用取余就可以了 小老鼠4个按键为一组按,不论多少次都是这样循环的顺序 直接 81 % 4 = 1
> 也就是最后一组没全按过来 只按了前 1 个 因此是 A 按键
> 但是 `Caps Lock` 会切换中英文大小写!第一轮循环是大写 第二轮循环是小写,我们需要计算当前是第几轮循环
> 直接 81/4+1 = 21 是奇数,因此大写
> 选 A
----
### 7,根节点深度为 0,一棵深度为 h 的满 k(k>1)叉树,即除最后一层无任何子节点外,其余每一层上的所有节点都有 k 个子节点的树,共有( )个节点。
A. (k^(h+1)-1)/(k-1)
B. k^h-1
C. k^h
D. (k^(h-1))/(k-1)
> 满K叉树,叉长满了!比如满二叉树就是完整的二叉树,节点数可以在这里算一算,第一层1个,第二层2个,第三层4个,第四层8,第n层2n个
> 只需要将他们累加就好了 那么 是不是等比数列求和,等比为 2,2在题目中是 k
> 答案:Sh = “k 的 (h+1) 次方减去 1,再除以 (k 减 1)” 因此选择 A
----
### 8,在以下排序算法中,不需要进行关键字比较操作的算法是( )。
A. 基数排序
B. 冒泡排序
C. 堆排序
D. 直接插入排序
> 基数排序 相当于不是比较整体大小 而是比较某个位的大小,是对关键字的一部分进行比较,关键字我们可以理解为就是被排序的元素,比如 `123 > 100` 里面的123和100就是关键字
----
### 9,给定一个含 N 个不相同数字的数组,在最坏情况下,找出其中最大或最小的数,至少需要 N-1 次比较操作。最坏情况下,在该数组中同时找最大与最小的数至少需要( )次比较操作。([ ] 表示向上取整,{ } 表示向下取整)
A. [3N/2]-2
B. {3N/2}-2
C. 2N-2
D. 2N-4
> 我们可能会想到 2N-2 这的确可以,但不是最优解法,如果我们用下面的方法解题呢
>每次取两个数,先在它们之间比较一次,分出“较大者”和“较小者”
然后:
把“较大者”去挑战当前的最大值
把“较小者”去挑战当前的最小值
> 这样,每两个数,我们只用 3 次比较:
两数之间比 1 次
较大者 vs 当前最大 → 1 次
较小者 vs 当前最小 → 1 次
> 又因为 第一对不需要和“当前最值”比(因为第一次取值,最值还没初始化),所以可以省 2 次
> 因此有 n 个数的时候。我们需要比较 3N/2-2 次,至于取整,我们直接代入一下就可以了
> 比如我们排序的数组 [2,1] 如果向下取整 3/2-2 中,如果3/2向下取整,就是小于0次了,很显然不对
> 因此选 A
----
### 10,下面的故事与( )算法有着异曲同工之妙。
从前有座山,山里有座庙,庙里有个老和尚在给小和尚讲故事:“从前有座山,山里有座庙,庙里有个老和尚在给小和尚讲故事:‘从前有座山,山里有座庙,庙里有个老和尚给小和尚讲故事……’。”
A. 枚举
B. 递归
C. 贪心
D. 分治
> 直接循环
----
### 11,由 4 个没有区别的点构成的简单无向连通图的个数是( )。
A. 6
B. 7
C. 8
D. 9
> 无向连通图,意味着每个元素都是和某个元素相互链接的,问的就是 4 个元素有多少种链接方法 总共6中,直接枚举出结果
> 各种链接方法如下(懒得看就直接记住表格)
| n(顶点数) | 连通图个数 |
|------------|-------------|
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | **6** |
| 5 | 21 |
| 6 | 112 |
| 7 | 853 |
| 8 | 11117 |
```
●-●-●-●
●
/ | \
● ● ●
●-●
| |
●-●
●
|
●
/ \
● ●
●
|
●
/ \
●--●
●
/ \
/ \
●-----●
\ /
\ /
●
●
/|\
/ | \
●---|---●
\ | /
\ | /
●
```
----
### 12,设含有 10 个元素的集合的全部子集数为 S,其中由 7 个元素组成的子集数为 T,则 T / S 的值为( )。
A. 5 / 32
B. 15 / 128
C. 1 / 8
D. 21 / 128
> 一个含有 n 个元素的集合,其所有子集的个数是 2^n 因为最小的集合也需要2个元素
> 由 7 个元素组成的子集数,就是从 10 个元素中选出 7 个的元素的排列组合数 组合数公式写法如下

> 计算出 S=1024 T=120 因此 120/1024 = 60/512 = 30/256 = 15/128 选择 B
----
### 13,10000 以内,与 10000 互质的正整数有( )个。
A. 2000
B. 4000
C. 6000
D. 8000
> 如果两个数没有除了 1 以外的公因数(即没有大于 1 的公因数),那么它们就是互质的
> 事实上 欧拉总结了一个公式
在 1 到 n 的正整数中,与 n 互质(即最大公约数为 1)的数的个数 记作 ϕ(n)。
关于如何计算 ϕ(n) 我们在这里展示欧拉公式全貌
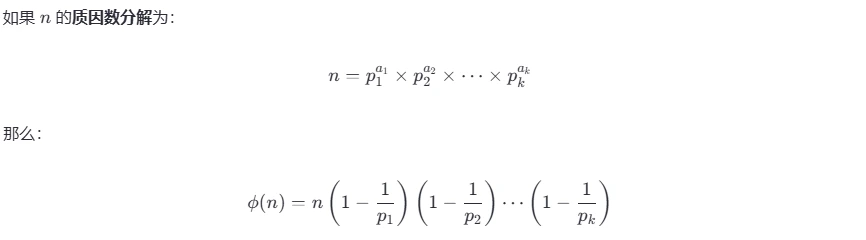
> n 是数字个数
> 为了使用欧拉公式,我们需要分解质因数,分解因数的方法可以看文章:https://www.lingyuzhao.top/b/Article/-6981103327968397
> 10000 的质因数分解如下 10000=2^4 × 2^5
> 因此 p1是2 p2是5
> 代入欧拉
----
### 14,为了统计一个非负整数的二进制形式中 1 的个数,代码如下:
```
int CountBit (int x)
{
int ret = 0;
while (x)
{
ret++;
___________;
}
return ret;
}
```
则空格内要填入的语句是( )。
A. x >>= 1
B. x &= x - 1
C. x |= x >> 1
D. x <<= 1
> 我们要在 while(x) 循环中:
每次发现一个 1,就 ret++
然后把这个 1 从 x 中去掉,避免重复计数
直到 x 变成 0,循环结束
> 因此题目考察的就是如何去掉二进制数据的最低位的 1 直到 x 变为0
> 在下面举了一个例子
```
x = 12 = 1100
while(12) 进循环
x - 1 = 11 = 1011
↓ 按位与
x & (x-1) 1000 → 去掉了最右边的 1
```
然后下一轮
```
x = 8 = 1000
while(8) 进循环
x - 1 = 7 = 111
↓ 按位与
x & (x-1) 0000 → 去掉了最右边的 1
```
然后下一轮
```
while 不进循环 统计结果为 2
```
----
### 15,下图所使用的数据结构是( )。
A. 哈希表
B. 栈
C. 队列
D. 二叉树
> 略 没什么好说的
----
### 16,(5分)甲乙丙丁四人在考虑周末要不要外出郊游。
已知:①如果周末下雨,并且乙不去,则甲一定不去;②如果乙去,则丁一定去;③如果丙去,则丁一定不去;④如果丁不去,而且甲不去,则丙一定不去。
根据如上叙述,请选择:
如果周末丙去了,则甲(1),乙(2),丁(3),周末(4)。
A. 没去;去了;去了;下雨
B. 没去;没去;去了;下雨
C. 去了;去了;没去;没下雨
D. 去了;没去;没去;没下雨
> 直接枚举排除 选D
----
### 17,(5分)从1到2018这2018个数中,共几个包含数字8的数。包含数字8的数是指有某一位是“8”的数,例如“2018”与“188”。
A. 562
B. 543
C. 602
D. 544
> 先算不包含 8 的数字有多少
> 每个位可以是 0~9,但不能是 8 → 每位有 9 种选择(0,1,2,3,4,5,6,7,9)
> 直接将千位不同的值的情况有多少8列举出来
> 千位是 0 的情况 也就是有3个位,这个时候不含8的数值总共有 9x9x9个组合 = 729
> 但是我们这样的计算 把000 也算进去了 从1开始才行,所以最后结果是 728
> 千位是 1 的情况 其实还是 729 因为千位是 1 所以 1000 也是允许的了
> 千位是 2 的情况 一样,但是!2018是最大值,因此这里相当于是只有 2 个值含8,分别是 8 和 18,因此不含8的数有18-2个
> 最终汇总不含8的数值有 728 + 729 + 16 = 1473
> 那么最终含 8 的数值数量就是 2018-1473=544 选D
----
```
#include <cstdio>
char st[100];
int main() {
scanf("%s", st);
for (int i = 0; st[i]; ++i) {
if ('A' <= st[i] && st[i] <= 'Z')
st[i] += 1;
}
printf("%s\n", st);
return 0;
}
```
## 代码阅读选择题
### 18, 输入:QuanGuoLianSai
输出:_________
A. QuanGuoLianSai
B. RuanGuoLianSai
C. RuanHuoMianTai
D. QuanHuoMianTai
> 如果是大写就 + 1 因此 AD排除,且Lian不可能,应该是Mian 选 C
----
### 19, 输入:15
```
#include <cstdio>
int main() {
int x; scanf("%d", &x); int res = 0;
for (int i = 0; i < x; ++i) {
if (i * i % x == 1) ++res;
}
printf("%d", res);
return 0;
}
```
输出:________
A.4
B.6
C.8
D.9
> 计算 0到14中 有多少数值满足 i^2%x == 1
> 满足条件的 i 有 `1,4,11,14` 共4个,选 A
----
### 20, 输入:5 6
```
#include <iostream>
using namespace std;
int n, m;
int findans(int n, int m) {
if (n == 0) return m;
if (m == 0) return n % 3;
return findans(n - 1, m) - findans(n, m - 1) + findans(n - 1, m - 1);
}
int main() {
cin >> n >> m;
cout << findans(n, m) << endl;
return 0;
}
```
输出:________
A. 5
B. 8
C. 2
D. 11
> 代码中可以看递推公式:F(n, m) = F(n-1, m) + F(n-1, m-1) - F(n, m-1)
> 接下来我们只需要列个表 行代表 n 列代表 m 的值
> n的取值范围是 0到5,m的取值范围是 0到6
| n\m | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| :------------: | :------------: | :------------: | :------------: | :------------: | :------------: | :------------: | :------------: |
| 0 | | | | | | | |
| 1 | | | | | | | |
| 2 | | | | | | | |
| 3 | | | | | | | |
| 4 | | | | | | | |
| 5 | | | | | | | |
> 然后依次计算出每个单元格的值就好,比如 F(0,0)的时候计算结果是0,F(0,1) 计算结果是1
> 然后计算出 F(1,0) 答案都是 1
> 继续计算出 F(2,0) 答案都是 2 F(3,0) 都是0
| n\m | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| :------------: | :------------: | :------------: | :------------: | :------------: | :------------: | :------------: | :------------: |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | | | | | | |
| 2 | 2 | | | | | | |
| 3 | 0 | | | | | | |
| 4 | 1 | | | | | | |
| 5 | 2 | | | | | | |
> 我们可以直接套公式一步步进行递归 好理解 但是效率不高,所以用另一种方法!直接进行填表
我们按行计算,每行从 `m=1` 开始往右算。
🔹 计算第 1 行(n=1)
公式:`F(1, m) = F(0, m) - F(1, m-1) + F(0, m-1)`
- `F(1,1)` = F(0,1) - F(1,0) + F(0,0) = 1 - 1 + 0 = **0**
- `F(1,2)` = F(0,2) - F(1,1) + F(0,1) = 2 - 0 + 1 = **3**
- `F(1,3)` = 3 - 3 + 2 = **2**
- `F(1,4)` = 4 - 2 + 3 = **5**
- `F(1,5)` = 5 - 5 + 4 = **4**
- `F(1,6)` = 6 - 4 + 5 = **7**
更新表格:
| n\m | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|-----|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 0 | 3 | 2 | 5 | 4 | 7 |
| 2 | 2 | | | | | | |
| 3 | 0 | | | | | | |
| 4 | 1 | | | | | | |
| 5 | 2 | | | | | | |
---
🔹 计算第 2 行(n=2)
公式:`F(2, m) = F(1, m) - F(2, m-1) + F(1, m-1)`
- `F(2,1)` = F(1,1) - F(2,0) + F(1,0) = 0 - 2 + 1 = **-1**
- `F(2,2)` = 3 - (-1) + 0 = **4**
- `F(2,3)` = 2 - 4 + 3 = **1**
- `F(2,4)` = 5 - 1 + 2 = **6**
- `F(2,5)` = 4 - 6 + 5 = **3**
- `F(2,6)` = 7 - 3 + 4 = **8**
更新:
| n\m | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|-----|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 0 | 3 | 2 | 5 | 4 | 7 |
| 2 | 2 | -1| 4 | 1 | 6 | 3 | 8 |
| 3 | 0 | | | | | | |
| 4 | 1 | | | | | | |
| 5 | 2 | | | | | | |
---
🔹 计算第 3 行(n=3)
公式:`F(3, m) = F(2, m) - F(3, m-1) + F(2, m-1)`
- `F(3,1)` = F(2,1) - F(3,0) + F(2,0) = (-1) - 0 + 2 = **1**
- `F(3,2)` = 4 - 1 + (-1) = **2**
- `F(3,3)` = 1 - 2 + 4 = **3**
- `F(3,4)` = 6 - 3 + 1 = **4**
- `F(3,5)` = 3 - 4 + 6 = **5**
- `F(3,6)` = 8 - 5 + 3 = **6**
→ 发现:**F(3, m) = m**
更新:
| n\m | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|-----|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 0 | 3 | 2 | 5 | 4 | 7 |
| 2 | 2 | -1| 4 | 1 | 6 | 3 | 8 |
| 3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | | | | | | |
| 5 | 2 | | | | | | |
---
🔹 计算第 4 行(n=4)
公式:`F(4, m) = F(3, m) - F(4, m-1) + F(3, m-1)`
- `F(4,1)` = 1 - 1 + 0 = **0**
- `F(4,2)` = 2 - 0 + 1 = **3**
- `F(4,3)` = 3 - 3 + 2 = **2**
- `F(4,4)` = 4 - 2 + 3 = **5**
- `F(4,5)` = 5 - 5 + 4 = **4**
- `F(4,6)` = 6 - 4 + 5 = **7**
→ **F(4, m) = F(1, m)**
更新:
| n\m | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|-----|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 0 | 3 | 2 | 5 | 4 | 7 |
| 2 | 2 | -1| 4 | 1 | 6 | 3 | 8 |
| 3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 0 | 3 | 2 | 5 | 4 | 7 |
| 5 | 2 | | | | | | |
---
🔹 计算第 5 行(n=5)
公式:`F(5, m) = F(4, m) - F(5, m-1) + F(4, m-1)`
- `F(5,1)` = F(4,1) - F(5,0) + F(4,0) = 0 - 2 + 1 = **-1**
- `F(5,2)` = 3 - (-1) + 0 = **4**
- `F(5,3)` = 2 - 4 + 3 = **1**
- `F(5,4)` = 5 - 1 + 2 = **6**
- `F(5,5)` = 4 - 6 + 5 = **3**
- `F(5,6)` = 7 - 3 + 4 = **8**
---
✅ 最终表格:
| n\m | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|-----|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 0 | 3 | 2 | 5 | 4 | 7 |
| 2 | 2 | -1| 4 | 1 | 6 | 3 | 8 |
| 3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 1 | 0 | 3 | 2 | 5 | 4 | 7 |
| 5 | 2 | -1| 4 | 1 | 6 | 3 | **8** |
---
最终答案:**F(5, 6) = 8**
### 21,输入 10 7 1 4 3 2 5 9 8 0 6
```
#include <cstdio>
int n, d[100];
bool v[100];
int main() {
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
scanf("%d", d + i);
v[i] = false;
}
int cnt = 0;
for (int i = 0; i < n; ++i) {
if (!v[i]) {
for (int j = i; !v[j]; j = d[j]) {
v[j] = true;
}
++cnt;
}
}
printf("%d\n", cnt);
return 0;
}
```
输出:________
A.10
B.2
C.4
D.6
> 首先输入每个数值之后,数值会被存储到d中,v会初始化一个布尔
> d = [7 1 4 3 2 5 9 8 0 6] v全是 false
> 在下面的循环中,会依次迭代每个d元素 并判断他们是否被访问过
> 如果v中判断当前元素没有被访问过 就使用奇怪的循环来将一些元素进行访问标记
> 最终计数结果才会出现,我们在这里进行推导
> 第一次外循环
>> 第一次内循环 j=0 然后将 v[0] 设置为 true 然后将 j 设置为 d[0]=7
>> 判断是否可以继续循环?v[7] 为false 可以继续循环
>> 第二次内循环 j=7 将 v[7] 设为 true 然后将 j 设置为 d[7]=8
>> 判断是否可以继续循环?v[8] 为false 可以继续
>> 第三次内存换 j=8 将 v[8] 设为 true 然后将 j 设置为 d[8] = 0
>> 判断是否可以继续循环?v[0] 为 false 不可以继续循环
>> cnt + 1 = 1
> 此时 v中的[0,7,8] 均为true
> 第二次外循环 v[1] 为false 没被访问过 可以循环
>> 第一次内 j=1 set v[1]=true set j=d[1]=1
>> 判断 v[1] 为 true 不可循环
>> cnt + 1 = 2
> 此时 v中的[0,1,7,8] 均为 true
> 第三次外循环 v[2] 为 false 没被访问过 可以循环
>> 第一次内 j=2 set v[2]=true set j=d[2]=4
>> 判断 v[4] 为 false 可循环
>> 第二次内 j=4 set v[4]=true set j=d[4]=2
>> 判断 v[2] 为 true 不可循环
>> cnt +1 = 3
> 此时 v中的[0,1,2,4,7,8] 均为 true
> 第四次外循环 v[3] 为 false 可循环
>> 第依次内 j=3 set v[3]=true set j=d[3]=3
>> 判断 v[3] 为 true 不可循环
>> cnt + 1 = 4
> 此时 v中的[0,1,2,3,4,7,8] 均为 true
> 第五次外循环 v[4] 为 true 不可循环
> 第六次外循环 v[5] 为 false 可循环
>> 第一次内 j=5 set v[5]=true set j=d[5]=5
>> 判断 v[5]为 true 不可循环
>> cnt + 1 = 5
> 此时 v中的[0,1,2,3,4,5,7,8] 均为 true
> 第七次外循环 v[6] 为 false 可循环
>> 第一次内 j=6 set v[6]=true set j=d[6]=9
>> 判断 v[9] 为 false 可循环
>> 第二次内 j=9 set v[9]=true set j=d[9]=6
>> 判断 v[6] 为 true 不可循环
>> cnt + 1 = 6
> 此时 v中的[0,1,2,3,4,5,6,7,8,9] 均为 true
> 第八次 九次 十次 循环都不能进入 没有第十一次循环了
> cnt 为 6
## 代码补全题
### 求解n的所有约数两两之间最大公约数的和对10007取余后的值
(一)(最大公约数之和)下列程序想要求解整数 n 的所有约数两两之间最大公约数的和对 10007 求余后的值,试补全程序。(第一小题 2 分,其余每小题 3 分)
举例来说,4 的所有约数是 1,2,4。1 和 2 的最大公约数为 1;2 和 4 的最大公约数为 2;1 和 4 的最大公约数为 1。于是答案为 1+2+1=4。
要求 getDivisor 函数的复杂度为 O(√n),gcd 函数的复杂度为 O(log max(a,b))。
```
#include <iostream>
using namespace std;
const int N = 110000, P = 10007;
int n;
int a[N], len;
int ans;
void getDivisor() {
len = 0;
for (int i = 1; __①__ <= n; ++i)
if (n % i == 0) {
a[++len] = i;
if (__②__ != i) a[++len] = n / i;
}
}
int gcd(int a, int b) {
if (b == 0) {
__③__;
}
return gcd(b, __④__);
}
int main() {
cin >> n;
getDivisor();
ans = 0;
for (int i = 1; i <= len; ++i) {
for (int j = i + 1; j <= len; ++j) {
ans = (__⑤__) % P;
}
}
cout << ans << endl;
return 0;
}
```
#### 最大公约数函数解析 - gcd
> 公约数就是可以同时被两个数字整除的数,比如 2 6 的公约数有 1 2 ,最大公约数就是取个最值,为 2
gcd 函数是求解最大公约数的,根据名字可以猜到,最大公约数的计算方法我们可以使用欧几里得公式
```
# 此公式为辗转相除法,意味着不断的求解 a/b 后还剩下多少,如果不剩下值 也就是 b 为0,则代表公约数就是a
gcd(a,b) = b == 0 ? a : gcd(b, a%b)
```
>举例说明:
>计算 gcd(48, 18):
>>gcd(48, 18) → 48 % 18 = 12 → gcd(18, 12)
>>gcd(18, 12) → 18 % 12 = 6 → gcd(12, 6)
>>gcd(12, 6) → 12 % 6 = 0 → gcd(6, 0)
>>b == 0,返回 a = 6
>>所以,gcd(48, 18) = 6。
#### 找到某个数值的所有约数 - getDivisor
> 约数就是可以整除的数,比如 6 的约数 有 1 2 3 6
此公式的本质就是判断从 1 到 n 中的每个数值,设数值为 i,看看谁可以满足 n%i==0,满足的就代表 i 是n的约数
#### 对代码进行解析
##### 22,①处应填( )。
A. i
B. i×i
C. i+1
D. i-1
> 1号位置很明显就是迭代每个数值,但是题目要求时间复杂度为 O(根号n)
> 因此迭代的次数必须要是根号n才行
> 那我们如何让 i 的迭代变为根号n呢?
> 答案是在判断条件的位置给 n 做2次幂运算!
> 因此是 i×i 选择 B
##### 23,②处应填( )。
A. n+i
B. n-i
C. n*i
D. n/i
> 很显然这里是求解另一个约数的逻辑
> i 就是从 1 到 根号n 范围中的每个数字
> if n%i==0 是提取一个约数的判断条件 看看是否可以被整除
> 但是由于我们迭代范围只有 1到根号n 所以大于根号n的所有值都不会被 n%i 的逻辑判断
> 因此我们的循环中还有另一个 if 语句 用于提取到另一个约数 也就是大于根号n范围后面的因数
>> 接下来我们继续了解 当前 i 已经是约数了,那i什么情况下还可以n/i是约数呢?
>>> 9 的约数有 1 3 9
>>> 代入到这道题中,迭代范围只有 根号9,也就是i只有1,3 同时 n 是9
>>> 我们直接看看谁代入到哪个选择中符合条件就好咯
>>>代入约数 1 也就是 i=1
>>>> n+i = 9+1 = 10 != 1 n/i=9/1=9 满足约数
>>>> n-i = 9-1 = 8 != 1 n/i=9/1=9 满足约数
>>>> n×i = 9×1 = 9 != 1 n/i=9/1=9 满足约数
>>>> n/i = 9/1 = 9 != 1 n/i=9/1=9 满足约数
>>>> 看来代入约数 1 无法判断那个条件适合放到第二个 if
>>> 代入约数 3 也就是 i=3
>>>> n+i = 9+3 = 12 != 3 n/i=9/3=3 满足约数 但是上面已经追加过了
>>>> n-i = 9-3 = 6 != 3 n/i=9/3=3 满足约数 但是上面已经追加过了
>>>> n×i = 9×3 = 27 != 3 n/i=9/3=3 满足约数 但是上面已经追加过了
>>>> n/i = 9/3 = 3 != 3 这个不满足条件 不会被追加 正好符合我们的意向 避免重复追加约数,且在 i=1 的时候能够筛选出我们需要的值
> 最终选择 D
##### 24,③处应填( )。
A. return b/a
B. return gcd(a, b)
C. return b
D. return a
> 3的位置属于求解最大公约数范围,我们知道求解最大公约数的时候 如果其中一方为0,意味着此时不为0的一方就是最大公约数了,因此这里我们 b为0 a就是最大公约数 选择 D
##### 25,④处应填( )。
A. a%b
B. a-b
C. b%a
D. b-a
> 这里我们知道 为了能够不断的求解公约数,本质上就是不断的对当前两个操作数的商继续进行除法计算,得到除不尽的余数,所以这里一定是取余符号
> 而我们这里的底层原理其实就是 把 原来的除数 b 变成下一轮的被除数,把 余数 a % b 变成下一轮的除数。直到其中的被除数为0 不能继续除了。
> 因此这个位置要选择 A
##### 26,⑤处应填( )。
A. ans + gcd(i, j)
B. gcd(i, j)
C. ans + gcd(a[i], a[j])
D. gcd(a[i], a[j])
> 这里就是如何调用了,题意要求 `求解整数 n 的所有约数两两之间最大公约数的和对 10007 求余后的值` 而 P 就是 10007,因此这个位置一定就是 n 的所有约数两两之间的最大公约数之和
> 因为 i j 是索引,而我们要做的是将所有约数两两之间的最大公约数计算到,而约数被存储到了A中,因此不可能使用索引 A B 被排除了
> 又因为题目要求之和对10007取余 所以直接取 gcd 是不对的,肯定要将 gcd 的结果累加起来才行,所以 D被排除了
> 至于C为什么成立, m < n 且 m ≥ 0 的时候 m%n 的结果还是 m,因此 ans = (ans + gcd(a[i], a[j]))% 10007 z的结果一定是 ans + gcd(a[i], a[j]) 变相实现了累加
>> 如果 ans + gcd(a[i], a[j]) 比P大怎么办?
>> 没关系的哦,在代码里有个对P的取余操作 ans + gcd(a[i], a[j]))% 10007 不会比 10007 大!
>> 这道题选择 C
### 对于一个数列Q的元素在一个数列P中寻找合适的位置
对于一个1到n的排列P(即1到n中每一个数在P中出现了恰好一次),令q_i为第i个位置之后第一个比P_i值更大的位置,如果不存在这样的位置,则q_i=n+1。
举例来说,如果n=5且P为1 5 4 2 3,则q为2 6 6 5 6。
其中 2 是q的第一个元素,根据题意我们需要在 P 中从的第一个元素开始往后查找,第二个元素就是比 p[0]值更大的元素所在位置,因此返回 2
下列程序读入了排列P,使用双向链表求解了答案。试补全程序。(第二小题2分,其余每小题3分)
请注意,数据范围为1 ≤ n ≤ 10^5。
```
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int L[N], R[N], a[N];
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) {
int x;
cin >> x;
// __①__ 处应填什么?
}
for (int i = 1; i <= n; ++i) {
R[i] = // ②处应填什么?
L[i] = i - 1;
}
for (int i = 1; i <= n; ++i) {
L[// ③处应填什么?] = L[a[i]];
R[L[a[i]]] = R[// ④处应填什么?];
}
for (int i = 1; i <= n; ++i) {
cout << // ⑤处应填什么? << " ";
}
cout << endl;
return 0;
}
```
思考方法
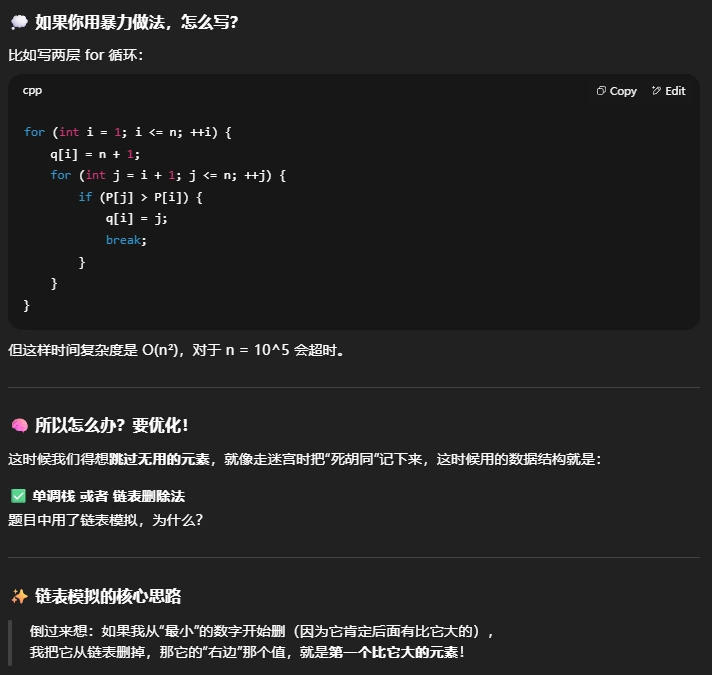
关于题的双向链表 L R 是如何构造的?
```
L 当前 R
[ 0 ] ←→ [ 1 ] ←→ [ 2 ] ←→ [ 3 ] ←→ [ 4 ] ←→ [ 5 ] ←→ [ 6 ]
↑ ↑ ↑ ↑ ↑
| | | | |
值1 值5 值4 值2 值3
```
运行逻辑可以使用下面的可视化了解
<iframe src='https://diskmirror.lingyuzhao.top/4/Binary/Article/Image/312551083605735/Test2.html' style='width:100vw;height:50vh'/>
| LR索引调用 | L\[i] | R\[i] |
| ---- | ----- | ----- |
| L[1] 和 R[1] | 0 | 2 |
| L[2] 和 R[2] | 1 | 3 |
| L[3] 和 R[3] | 2 | 4 |
| L[4] 和 R[4] | 3 | 5 |
| L[5] 和 R[5] | 4 | 6 |
> 这种题有一种共性,遇到双向列表大概率是这样设计的
i 是一个“值”,比如说是 4
那么 a[i] = a[4] = 3,代表 值为 4 的数出现在 P[3] 的位置
然后:
L[a[i]] = L[3] 就是 第 3 个位置左边的元素的位置
R[a[i]] = R[3] 就是 第 3 个位置右边的元素的位置
#### 27, ①处应填()。
A. a[x] = I
B. a[i] = x
C. L[i] = x
D. R[i] = x
> 这个部分属于数据的输入阶段,将p的进行构造存储
> 可以直接套上面的规则 A 选项正确
#### 28, ②处应填()。
A. a[i]+1
B. a[i]
C. i+1
D. a[i+1]
> 然后在这里套上面的规则,R 代表右边元素的位置,因此我们需要构建一下右边节点的元素,这里有两个是可能的答案
> a[i+1] 和 i+1
> 因为 双链表中的节点数组记录的是元素位置,格式如下
```
L[当前元素值]=当前元素值左边数值对应的索引
L[当前元素值]=当前元素值右边数值对应的索引
```
> 因此它不可能存储数值,而 2号位置是存储位,这里不应该是数值,是索引,选 C
#### 29, ③处应填()。
A. L[i]
B. L[a[i]]
C. R[i]
D. R[a[i]]
> 这部分属于删除链表中的节点,循环的时候 i 1到n 也就是从小到大开始删除
> 这很有利于我们的操作,如果 i 被删除的时候,获取到其右边有值,那么右边相邻这个位置就是比i更大的,因为比i小的都被删了
> 因此这里就是删除当前节点的操作
> 在双向链表中 删除当前节点,则当前左节点需要直接连接右节点
> 在这里的 i 是要删除的值 因此链表中的位置需要使用 a[i] 获取到
> 而 L[a[i]] 就是当前节点对应的链表中左邻元素的位置
> 因此可知 我们只需要让当前节点的右邻元素位置指向当前节点的左邻 就可以把当前位置移除
> 因为右邻节点位置是 R[a[i]] 的方法提取出来的 所以答案就是 D
> 其实本质是提取到当前元素右边最大的值的位置,但是由于右边可能包含比当前值小的,因此需要删除!
#### 30, ④处应填()。
A. i
B. a[i]
C. L[a[i]]
D. R[a[i]]
> 左边节点现在已经指向右边节点了 下一步就是让右边节点也移除a[i]
> 大概逻辑就是直接将 a[i] 的右边给 左节点的右节点
> 选择 B
#### 31, ⑤处应填()。
A. R[i]
B. L[i]
C. R[a[i]]
D. L[a[i]]
> 这里直接打印结果就行了,结果其实就是R的每个元素 选择 A
------
***操作记录***
作者:[zhao](https://www.lingyuzhao.top//index.html?search=4 "zhao")
操作时间:2025-08-04 22:02:38 星期一 【时区:UTC 8】
事件描述备注:保存/发布
中国 天津市 天津
[](如果不需要此记录可以手动删除,每次保存都会自动的追加记录)
