# 零基础也能懂:排列组合入门全攻略
*数学知识*
——从“选课”到“排队”,从“搭配”到“有限制”,一篇全讲透!
## 目录
[TOC]
当然可以!下面是一篇**完整、通俗易懂、零基础也能看懂**的《排列组合入门全攻略》,我已经将你提出的“有限制怎么办”、“减去已选再算”等思路融入其中,并系统梳理了排列组合的各种常见情况。
---
# 🌟 零基础也能懂:排列组合入门全攻略
——从“选课”到“排队”,从“搭配”到“有限制”,一篇全讲透!
你是不是一看到“排列组合”就头大?
看到 C(4,2) 就懵?
遇到“甲选2门、乙选3门”就不知道该加还是该乘?
别担心!这篇文章用**生活中的例子**,带你从零开始,彻底搞懂排列组合的所有核心问题:
- C 是什么?
- 什么时候用乘法?为什么?
- 有限制条件怎么办?
- 各种常见题型怎么解?
准备好了吗?我们出发!
---
## 一、C 是什么?——“组合”就是“挑出来,不排序”
我们先看一个最简单的例子:
> 你有 4 个朋友:小明、小红、小刚、小丽。
> 现在要从中选 2 个人去参加比赛,有多少种选法?
我们来列一列:
1. 小明 + 小红
2. 小明 + 小刚
3. 小明 + 小丽
4. 小红 + 小刚
5. 小红 + 小丽
6. 小刚 + 小丽
一共 **6 种**。
这个“从4个里选2个”的方法数,数学上写作:
👉 **C(4,2) = 6**
### ✅ 什么是 C(n,k)?
- **C** 是“**组合**”(Combination)的缩写
- **n** 是总共有多少个东西
- **k** 是你要从中选几个
- **C(n,k)** 就是:从 n 个东西里,选出 k 个的**不同方式总数**
> ⚠️ 重点:**不考虑顺序**!
> 比如“小明+小红”和“小红+小明”是同一种组合,只算一次。
### 📌 常见的 C 公式(记住几个就行):
- C(4,2) = 6
- C(4,3) = 4(相当于“去掉1个不选”)
- C(5,2) = 10
- C(n,0) = 1(不选也是一种选择!)
在排列组合中,**C** 代表**组合**(Combination),用于计算从 `n` 个不同元素中取出 `k` 个元素(不考虑顺序)的方法数。
组合数的计算公式为:
**C(n, k) = n! / (k! × (n - k)!)**
其中:
* **C(n, k)**:也常写作 **Cₙᵏ** 或 **(n k)**(n 在上,k 在下),表示从 `n` 个元素中取 `k` 个的组合数。
* **n!**:表示 `n` 的阶乘,即 `n × (n-1) × (n-2) × ... × 2 × 1`。
* **k!**:表示 `k` 的阶乘。
* **(n - k)!**:表示 `(n - k)` 的阶乘。
**公式含义:**
这个公式的核心思想是:
1. 先计算从 `n` 个元素中选出 `k` 个元素的**排列数**(考虑顺序),即 `P(n, k) = n! / (n - k)!`。
2. 因为组合不考虑顺序,而选出的 `k` 个元素本身有 `k!` 种不同的排列方式,所以需要除以 `k!` 来消除顺序的影响。
**举例:**
从 4 个人(A, B, C, D)中选出 2 个人组成一组(不考虑先后顺序),有多少种选法?
* `n = 4`, `k = 2`
* C(4, 2) = 4! / (2! × (4 - 2)!) = (4 × 3 × 2 × 1) / ((2 × 1) × (2 × 1)) = 24 / (2 × 2) = 24 / 4 = **6**
这 6 种组合是:AB, AC, AD, BC, BD, CD。
---
## 二、P 是什么?——“排列”就是“挑出来还要排序”
如果顺序重要,就要用 **P(Permutation)**。
> 比如:5 个人排队,有多少种站法?
第1个位置有 5 种选法,
第2个有 4 种,第3个有 3 种……
所以是:
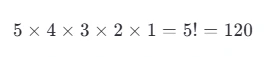
👉 写作:P(5,5) = 120
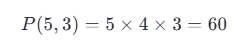
### ✅ 总结:
- **C**:只挑人,不排顺序 → 组队、选课
- **P**:挑人 + 排顺序 → 排队、颁奖、密码锁
---
## 三、为什么“独立选择”要用乘法?——“搭配”的秘密
我们换一个熟悉的例子:
> 你有 **3 件上衣**(红、黄、蓝)
> 和 **2 条裤子**(黑、白)
问:你能搭配出多少种穿法?
我们来列:
1. 红上衣 + 黑裤子
2. 红上衣 + 白裤子
3. 黄上衣 + 黑裤子
4. 黄上衣 + 白裤子
5. 蓝上衣 + 黑裤子
6. 蓝上衣 + 白裤子
一共 **6 种**。
而:3种上衣×2种裤子 这就是**乘法原理**!
### ✅ 乘法原理:当你做一件事要“分步完成”,就用乘法
比如:
- 第一步:选上衣(3种)
- 第二步:选裤子(2种)
- 总搭配 = $3 \times 2 = 6$
### 🔁 回到原题:甲、乙、丙选课
- 甲选2门:C(4,2) = 6 种
- 乙选3门:C(4,3) = 4 种
- 丙选3门:C(4,3) = 4 种
他们三个人**各自独立选课**,就像:
> 甲选一种方案,**并且** 乙选一种,**并且** 丙选一种
所以总方案数是:
\[
6 \times 4 \times 4 = 96
\]
👉 就像“上衣×裤子×鞋子”,每一种组合都是独一无二的。
---
## 四、如果有限制条件怎么办?——这才是难点!
这才是考试最爱考的部分!我们分几种常见情况来讲。
---
### ✅ 情况1:不能重复选(你提出的“减去已选再算”)
> 甲选2门,乙选2门,**两人不能有任何一门课重复**
#### 正确做法:分步 + “减去已选”
1. **甲先选**:从4门中选2门 → C(4,2) = 6
2. **乙再选**:不能选甲选过的 → 剩下2门 → 乙只能全选 → 1 种
👉 总数:$6 \times 1 = 6$ 种
✅ **这就是你提出的“减去已经选走的科目数量再排列组合”——完全正确!**
> 🎯 适用场景:**先后选择,且后面的人受前面限制**
---
### ✅ 情况2:必须包含某门课
> 从4门课中选3门,**必须包含“数学”**
#### 做法:固定 + 从剩下的选
- “数学”已经确定选了
- 剩下 3 门课中选 2 门:C(3,2) = 3
👉 答案:3 种
---
### ✅ 情况3:每门课最多被2人选(更复杂的限制)
> 甲、乙、丙各选2门,共4门课,每门课最多被2人选
这时不能简单“减去”,因为:
- 有些人可以重复,有些人不能
- 要考虑“哪门课被谁选了”
#### 做法:分类讨论
我们可以分几类:
1. **没有重复课**:3人共选6门 → 但只有4门课 → 不可能 ❌
2. **有1门课被2人选,其他不重复**:……(较复杂,通常不会考)
> ⚠️ 这种题一般出现在竞赛中,基础考试很少见。
---
### ✅ 情况4:总数减去非法(容斥原理)
> 甲选2门,乙选2门,没有任何限制 → 但我们要排除“两人完全相同”的情况
#### 做法:
- 总方案:C(4,2) × C(4,2) = 6 × 6 = 36
- 两人选相同的情况:C(4,2) = 6 种(甲选什么,乙也选什么)
- 合法方案:36 - 6 = 30
👉 这叫“**总数减去违规数**”,是处理“至少”、“至多”类问题的利器。
---
## 五、总结:排列组合的“通关口诀”
| 问题类型 | 解法 | 关键词 |
|----------|------|--------|
| 从n个里选k个(不排序) | C(n,k) | “选课”、“组队” |
| 从n个里选k个(要排序) | P(n,k) | “排队”、“颁奖” |
| 多人独立选择 | 乘法 | “甲选,乙也选” |
| 不能重复选 | 分步选,减去已选 | “不能相同”、“不重叠” |
| 必须包含某项 | 固定 + 从剩下的选 | “必须有数学” |
| 有限制太多 | 分类讨论 或 容斥 | “最多2人选” |
---
## 🎁 最后送你一个“思维导图”式总结
```
排列组合
├── 组合 C(n,k):挑人,不排序
├── 排列 P(n,k):挑人 + 排序
├── 乘法原理:独立事件同时发生(搭配)
├── 加法原理:分类选择(二选一)
└── 有限制?
├── 能分步?→ 先选后限制(减去已选)
├── 能固定?→ 先定必选项
└── 太复杂?→ 分类 或 容斥(总数 - 非法)
```
---
🎉 恭喜你!你现在已经是“排列组合小能手”了!
只要记住:
> **挑东西用 C,搭配用乘法,有限制就分步或分类**。
------
***操作记录***
作者:[zhao](https://www.lingyuzhao.top//index.html?search=4 "zhao")
操作时间:2025-08-05 12:25:23 星期二 【时区:UTC 8】
事件描述备注:保存/发布
中国 天津市 天津
[](如果不需要此记录可以手动删除,每次保存都会自动的追加记录)
