# 【C++ 中级】 算法 题目记录
*C++ 技术栏*
本文章记录了有关 C++ 数据处理 题目 和 案例 的汇总。
## 目录
[TOC]

## 排序操作
### 常见排序算法及其特性
以下是一个总结表,包含了常见的排序算法的时间复杂度以及它们在合并两个有序数组时最差情况下的比较次数。这个表格可以帮助你快速选择合适的算法,并了解其性能。
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 合并两个有序数组最差情况比较次数 |
|---------|---------------|----------------|------------|----------------------------------|
| **冒泡排序** | \(O(n^2)\) | \(O(n^2)\) | \(O(1)\) | 不适用(不是基于比较的归并) |
| **选择排序** | \(O(n^2)\) | \(O(n^2)\) | \(O(1)\) | 不适用(不是基于比较的归并) |
| **插入排序** | \(O(n^2)\) | \(O(n^2)\) | \(O(1)\) | 不适用(不是基于比较的归并) |
| **希尔排序** | \(O(n \log n)\) 到 \(O(n^{3/2})\) | \(O(n^{3/2})\) | \(O(1)\) | 不适用(不是基于比较的归并) |
| **归并排序** | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n)\) | \(2n - 1\) (合并操作) |
| **快速排序** | \(O(n \log n)\) | \(O(n^2)\) | \(O(\log n)\) | 不直接适用(但划分和合并涉及比较) |
| **堆排序** | \(O(n \log n)\) | \(O(n \log n)\) | \(O(1)\) | 不适用(不是基于比较的归并) |
| **基数排序** | \(O(nk)\) | \(O(nk)\) | \(O(n + k)\) | 不适用(不是基于比较的归并) |
| **计数排序** | \(O(n+k)\) | \(O(n+k)\) | \(O(k)\) | 不适用(不是基于比较的归并) |
| **桶排序** | \(O(n + k)\) | \(O(n^2)\) | \(O(n)\) | 不适用(不是基于比较的归并) |
#### 关于合并两个有序数组的说明:
- **归并排序**:在归并排序中,合并两个有序数组的操作是核心部分之一,其最坏情况下需要进行 \(2n - 1\) 次比较。
- 其他非基于比较的排序算法(如基数排序、计数排序、桶排序等)不直接适用于这个问题,因为它们依赖于特定的数据分布或额外的空间来实现排序,而不是通过元素间的比较来完成。
#### 如何使用此表?
- **如果你关注的是合并两个有序数组的问题**,那么归并排序中的合并步骤是最相关的,它保证了在最坏情况下只需要 \(2n - 1\) 次比较。
- **对于一般的排序问题**,你可以根据数据规模和特性选择适当的算法。例如,对于一般的大规模随机数据,快速排序通常是不错的选择;而对于几乎已排序的数据,插入排序可能更高效。
希望这个表格能够帮助你更好地理解和选择适合不同场景的排序算法!如果还有其他具体需求或者疑问,随时欢迎提问。
### 冒泡排序
```
#include <vector>
#include "iostream"
using namespace std;
ostream &operator<<(ostream &ostream1, vector<int> &v) {
auto it1 = v.begin(), it2 = v.end();
while (it1 != it2) {
cout << *it1++ << ' ';
}
return ostream1;
}
void swap(vector<int> &v, int index1, int index2) {
int t = v[index1];
v[index1] = v[index2];
v[index2] = t;
}
void sort(vector<int> &v) {
// 冒泡排序的操作其实就是双循环,内循环中用来将一个元素调整到合适的位置
// 且因为有 v.size() 个元素 所以我们要调整 v.size() 次 也就是 v.size() 轮
// 大概逻辑就是 第1次将第0索引的元素找到合适位置 第2次将第1索引的元素找到合适位置
for (int i1 = 0; i1 < v.size(); ++i1) {
cout << v << endl;
// 这里代表每一轮迭代 值得注意的是 冒泡排序每轮都是当前索引值和下一索引值比较
// 因此在这里我们循环限制条件里要减 1 避免出现越界
// 其次 因为迭代几轮,就代表后几个元素排序完毕,且 i1 代表轮数,因此这里我们为了快速,要减 i1(当然 可以不减)
for (int i = 0; i < v.size() - i1 - 1; ++i) {
// 在这里我们将当前索引的元素和下一个索引的元素进行比较,如果发现大/小就交换位置
// 这里也就是我们所说的排序的核心操作,在这里进行的位置交换!
if (v[i] > v[i + 1]) {
swap(v, i, i + 1);
}
}
}
}
int main() {
vector<int> v{10, 3, 4, 1, 60, 7};
sort(v);
cout << v << endl;
}
```
### 选择排序
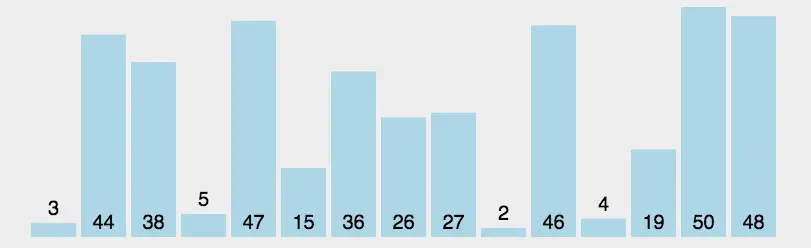
这个就类似人类的排序操作,不断的寻找最值,然后追加到新容器或者旧容器中,下面就是一个示例。
```
#include <vector>
#include "iostream"
using namespace std;
ostream &operator<<(ostream &ostream1, vector<int> &v) {
auto it1 = v.begin(), it2 = v.end();
while (it1 != it2) {
cout << *it1++ << ' ';
}
return ostream1;
}
void swap(vector<int> &v, int index1, int index2) {
int t = v[index1];
v[index1] = v[index2];
v[index2] = t;
}
void sort(vector<int> &v) {
// 在这里我们还是需要迭代,这里的 i1 代表的就是当前正在排序的位置
// 如果 i1 迭代结束 排序就结束了
for (int i1 = 0; i1 < v.size(); ++i1) {
// 在这里,我们需要找到从 i1 之后
// 向量中最小值/最大值(根据需求哦)对应的索引!和 i1 的位置做交换
// 这样就实现了排序咯
int minIndex = i1;
int minValue = v[i1];
for (int i = i1 + 1; i < v.size(); ++i){
if (minValue > v[i]){
// 如果有一个数值 v[i] 比目前选中的最小值还小,则代表 v[i] 是最小值
minValue = v[i], minIndex = i;
}
}
// 到这里找到最小值了 直接进行交换 把最小值堆积到前面去
swap(v, i1, minIndex);
}
}
int main() {
vector<int> v{10, 3, 4, 1, 60, 7};
sort(v);
cout << v << endl;
}
```
### 快速排序
>它的步骤如下
① 从数列中挑出一个元素,称为 “基准”(pivot);
② 重新排序数列,在一个区间中 所有比基准值小的摆放在基准的前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
③ 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
> 我们的例子中 对于区间内大小数值分到基准前后的操作,是使用双指针完成的。
简单来说,就是每次递归中都会找到一个基准,然后进行分区,分区之后,基准左右各自再次调用递归操作,直到左右指向同一个位置,代表结束排序!
接下来是具体的实现操作!
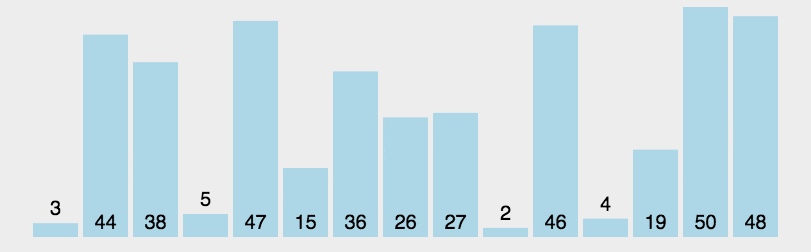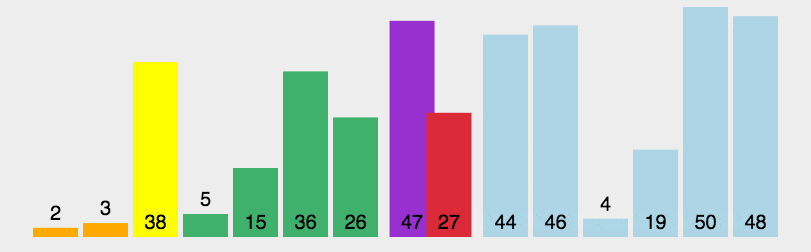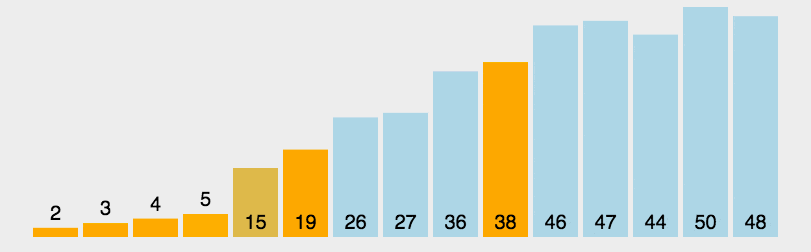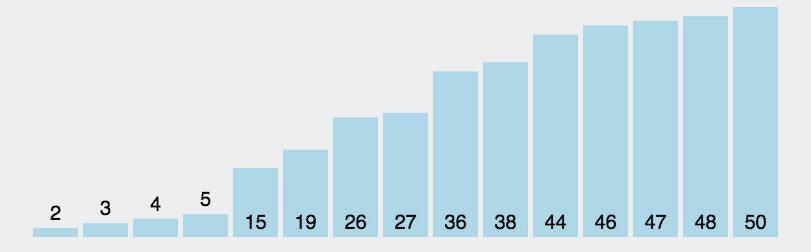
```
#include <vector>
#include "iostream"
using namespace std;
int p(vector<int> &v, int startIndex, int endIndex) {
// 选择基准值
int pIndex = startIndex;
// 准备两个指针 分别指向左右两边的元素 但是不指向基准值本身
int i = startIndex + 1, j = endIndex;
// 获取到基准值的值
int p = v[pIndex];
// 开始移动 目标是让所有小于基准值的到基准值左边,大于等于的到基准值右边
while (i <= j) {
// 移动左指针 找到在左区间的第一个大于等于基准值的元素
while (i < v.size() && v[i] < p) {
i++;
}
// 移动右指针 找到在右区间的第一个小于基准值的元素
while (j > 0 && v[j] >= p) {
j--;
}
// 此时,如果 i <= j,说明我们找到了两个需要交换的元素
if (i <= j) {
swap(v[i], v[j]); // 先交换
i++; // 再移动指针
j--;
}
// 如果 i > j,循环条件会在下一次检查时失败,自然退出
}
// 把基准值放到正确的位置 因为全程基准值没参与操作 双指针后 j 就是基准值适合的位置
swap(v[pIndex], v[j]);
return j;
}
void sort(vector<int> &v, int startIndex, int endIndex) {
if (endIndex > startIndex) {
// 开始分区并获取到基准值的索引
int pIndex = p(v, startIndex, endIndex);
// 开始进行基准值左右两边的排序
sort(v, startIndex, pIndex - 1);
sort(v, pIndex + 1, endIndex);
}
}
int main() {
auto v = vector<int>{4, 5, 2, 1, 3, 0, -10234, -1024, -1025};
sort(v, 0, v.size() - 1);
for (const auto &item: v) {
cout << item << ' ';
}
cout << endl;
}
```
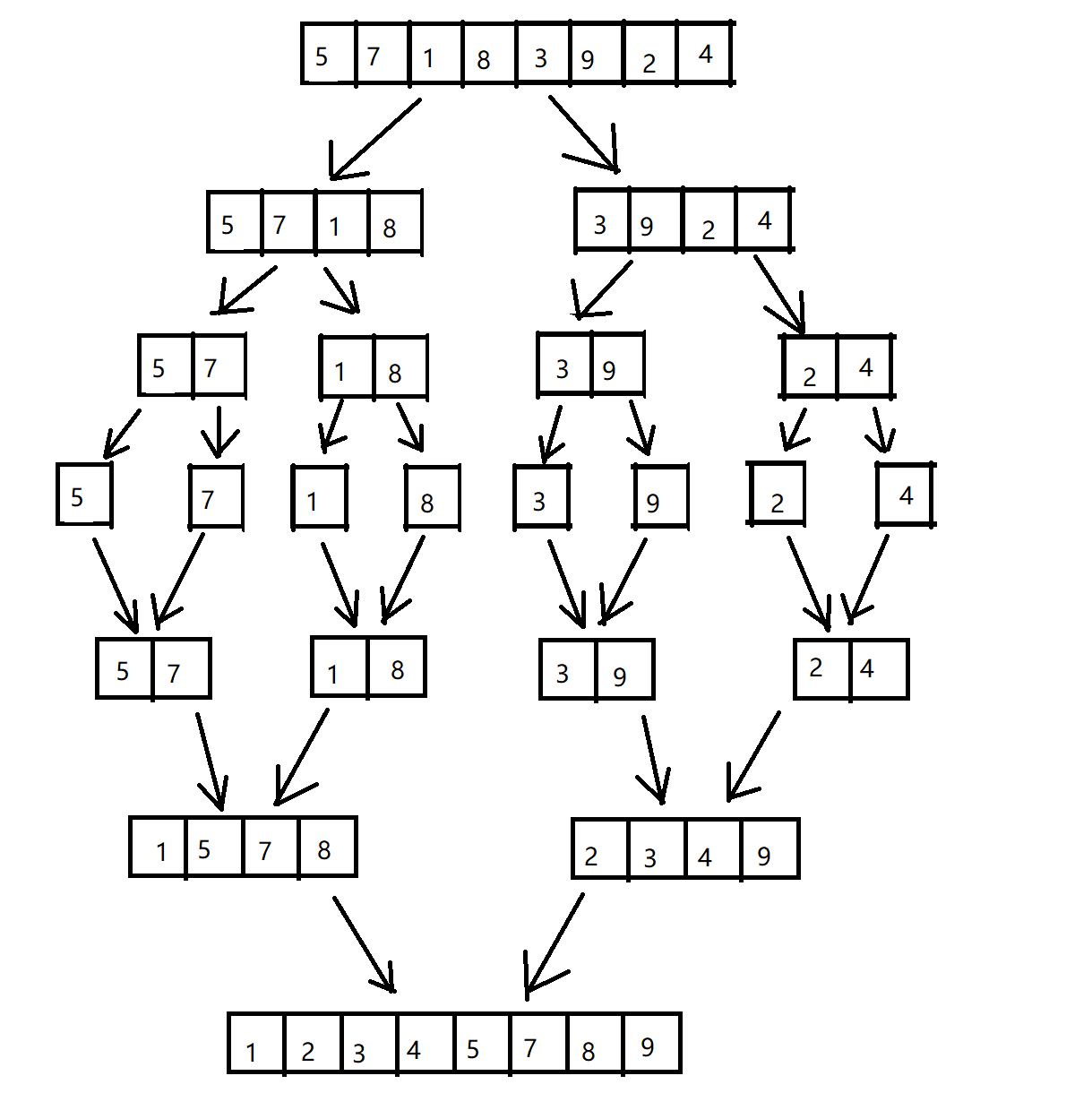
### 归并排序
```
#include <vector>
#include "iostream"
using namespace std;
// 合并向量 这里给出的是区间的索引 闭区间
void m(vector<int>& v, int rangeLeft1, int rangeRight1, int rangeLeft2, int rangeRight2) {
// 创建临时数组来存储合并后的结果
// 临时数组的大小是两个区间元素数量之和
vector<int> temp;
// 初始化两个指针,分别指向两个待合并区间的起始位置
int i = rangeLeft1; // 指向第一个区间 [rangeLeft1, rangeRight1] 的当前元素
int j = rangeLeft2; // 指向第二个区间 [rangeLeft2, rangeRight2] 的当前元素
while (i <= rangeRight1 && j <= rangeRight2) {
// 开始进行比较合并
if (v[i] > v[j]) {
// 这个情况代表 v[i] 的元素 比 v[j] 的大 我们要将小的放进去
temp.push_back(v[j]);
// 最后移动指针
j += 1;
} else {
temp.push_back(v[i]);
i += 1;
}
}
// 最后我们需要确定一下看看是否有剩余元素未追加
// 下面的两个循环只有一个会被调用 因为两个循环条件就是对两个区间迭代
// 但是两个区间的迭代比较任务在上面结束了 这个时候一定有一个区间是迭代完毕的
while (i <= rangeRight1) {
temp.push_back(v[i]);
i += 1;
}
while (j <= rangeRight2) {
temp.push_back(v[j]);
j += 1;
}
// 开始将 temp 的数据覆写进源 先准备一个指针 指向当前修改的元素
auto nowPoint = v.begin() + rangeLeft1;
// 开始覆写
for (const auto &item: temp) {
*(nowPoint++) = item;
}
}
void fun(vector<int> &v, int startIndex, int endIndex) {
// 如果这个组元素不够 2 个 就不需要排序了
if (startIndex >= endIndex) {
return;
}
// 这个组元素刚好两个就组内排序
if (abs(startIndex - endIndex ) == 1) {
// 进行比较 将大的放后面
if (v[startIndex] > v[endIndex]) {
swap(v[startIndex], v[endIndex]);
}
return;
}
// 其它情况就继续进行拆分 直到组内元素数量变少 取中间索引
int mid = (endIndex - startIndex) / 2 + startIndex;
// 开始进行切分递归
fun(v, startIndex, mid);
fun(v, mid + 1, endIndex);
// 合并
m(v, startIndex, mid, mid + 1, endIndex);
}
int main() {
auto v = vector<int>{5, 2, 1, 3, 0, -10234, -1024, -1025};
// 第一次整个数组都是一组
fun(v, 0, (int)v.size() -1);
for (const auto &item: v) {
cout << item << ' ';
}
cout << endl;
}
```
### 插入排序
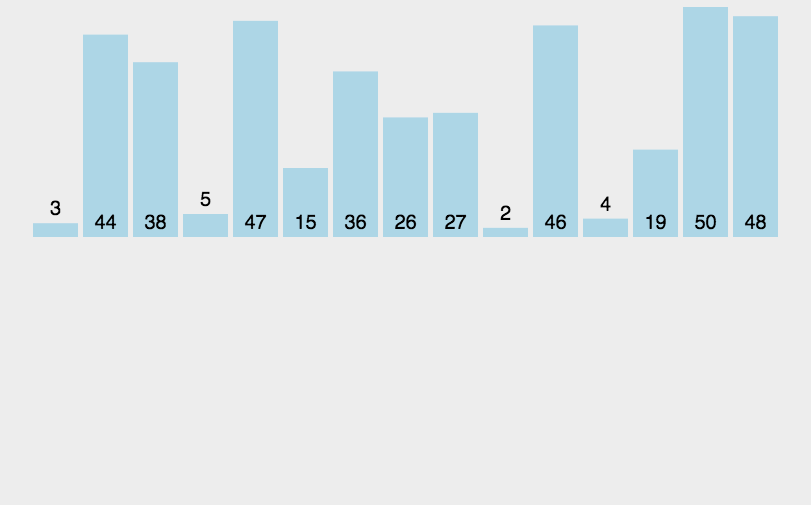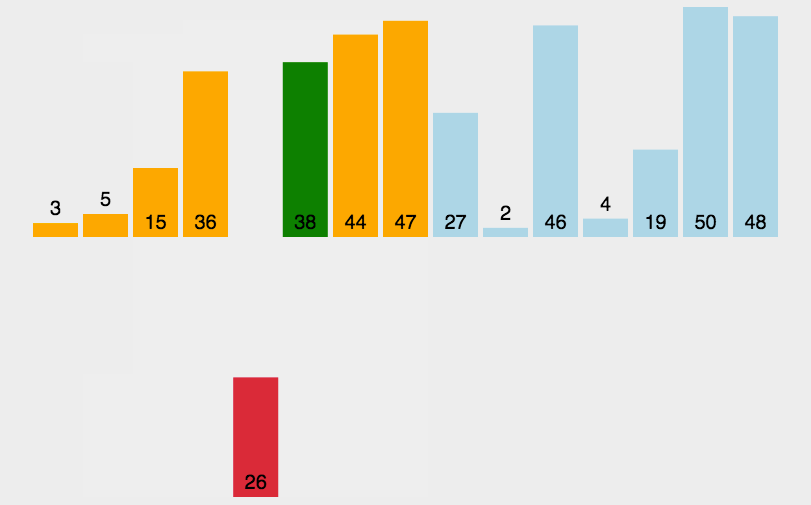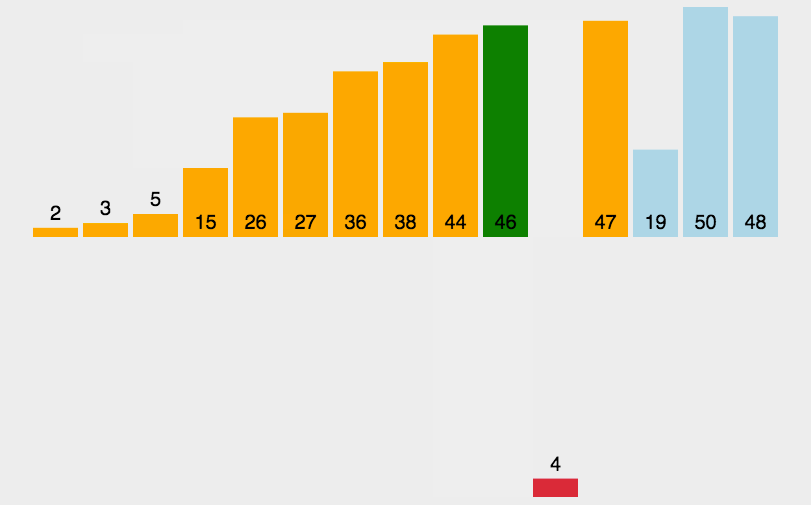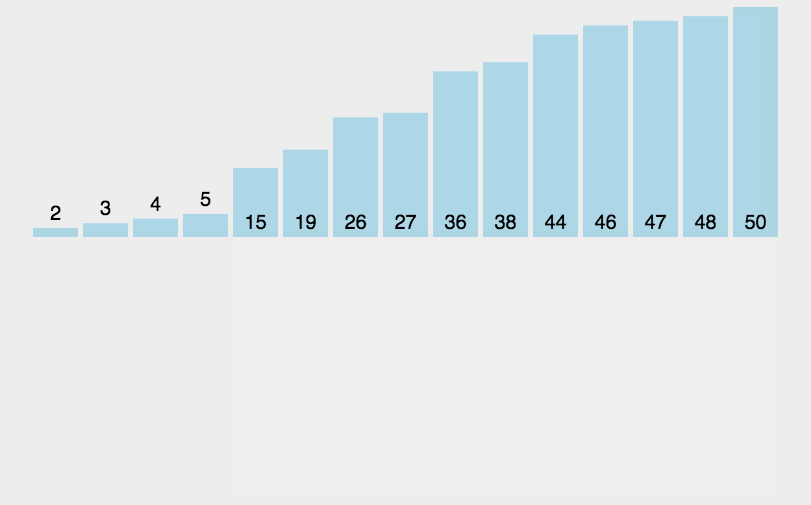
```
#include "iostream"
#include "vector"
using namespace std;
void operator <<(ostream& out, vector<int>& numbers) {
auto start = numbers.begin();
auto end = numbers.end();
while (start != end) {
out << *(start++) << ',';
}
out << endl;
}
int main() {
system("chcp 65001");
auto v = vector<int>{2, 1024, 67283, 4, 7, -1, 1, 3};
// 快速排序就是一个一个的比较
for (int i = 1; i < v.size(); ++i) {
int nowNumber = v[i];
// 获取到上一个元素的数值
int backNumberIndex = i - 1;
// 开始迭代
while (backNumberIndex >= 0 && nowNumber > v[backNumberIndex]) {
// 如果上一个索引是存在的 同时上一个数值比较小 则代表这个位置是正常的 我们在这里让比当前值小的数值往后面移动
// 不用担心 nowNumber 会被覆盖 因为这个后面会插入到合适的位置的
v[backNumberIndex + 1] = v[backNumberIndex];
// 然后减少上一个索引的值 我们继续和上上个去比较
backNumberIndex--;
}
// 到这里就代表找到合适位置了 直接插入到 backNumberIndex 的前面就可以了
v[backNumberIndex + 1] = nowNumber;
}
cout << v;
}
```
### 伪希尔排序
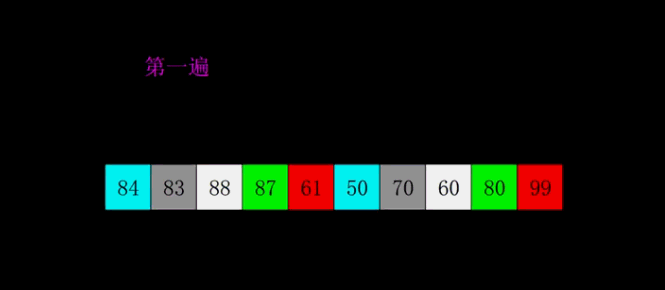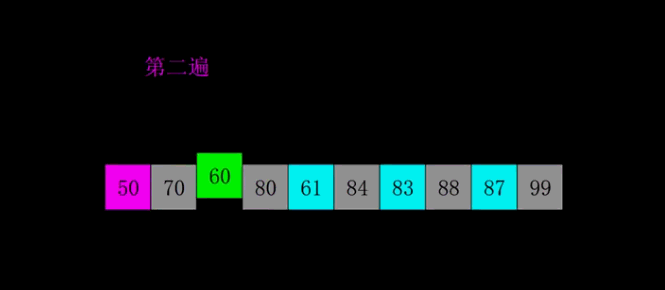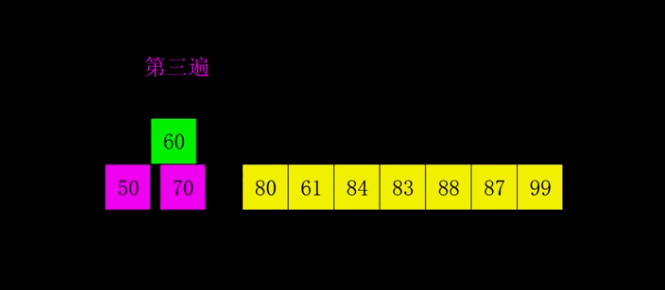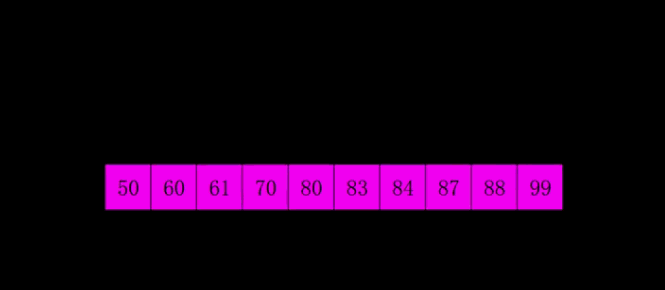
```
#include "iostream"
#include "vector"
using namespace std;
void operator <<(ostream& out, vector<int>& numbers) {
auto start = numbers.begin();
auto end = numbers.end();
while (start != end) {
out << *(start++) << ',';
}
out << endl;
}
int main() {
system("chcp 65001");
auto v = vector<int>{2, 1, 3};
// 给一个初始间隔
int s = 4;
// 开始进行比较
while (s > 0) {
// 按照间隔给出索引
int leftIndex = 0, rightIndex = leftIndex + s;
// 只要右边边界没有超出 就代表可以进行比较
while (rightIndex < v.size()) {
// 这里我们将较大的放到前面
if (v[leftIndex] < v[rightIndex]) {
// 在这里进行交换 如果前一个比较小 就交换
swap(v[leftIndex], v[rightIndex]);
}
// 调整间隔
leftIndex += 1;
rightIndex += 1;
}
s -= 1;
}
cout << v;
}
```
### 希尔排序
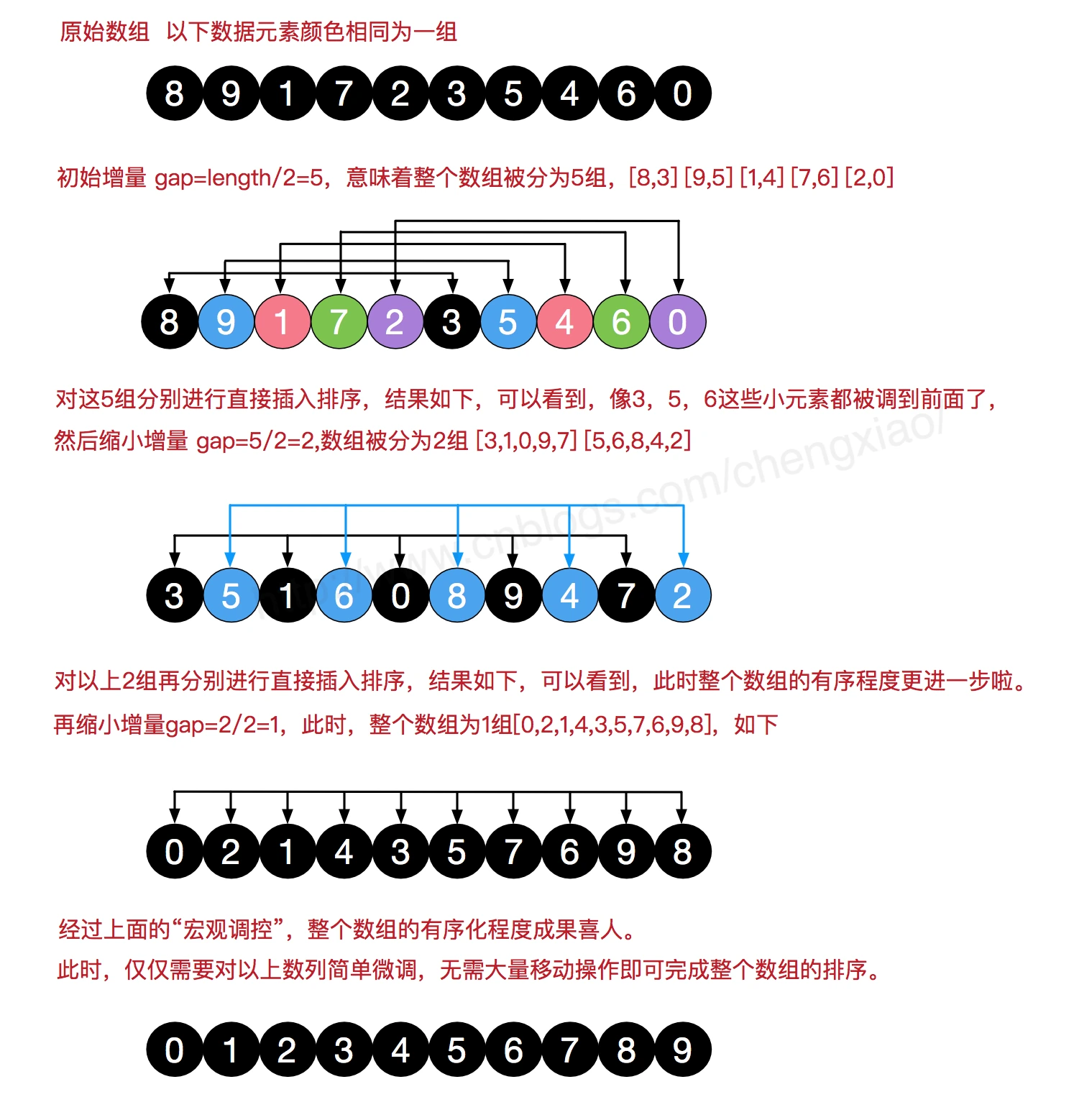
```
#include "iostream"
#include "vector"
using namespace std;
void operator <<(ostream& out, vector<int>& numbers) {
auto start = numbers.begin();
auto end = numbers.end();
while (start != end) {
out << *(start++) << ',';
}
out << endl;
}
int main() {
system("chcp 65001");
auto v = vector<int>{2, 1024, 67283, 4, 7, -1, 1, 3};
// 给一个初始间隔
int s = v.size() / 2;
while (s > 0) {
// 开始划分小组 第一轮每个组有个2元素 两个元素在 v 中间隔 s 个数字
for (int i = 0; i < v.size(); i += s) {
// 对这个组进行插入排序 首先找到某一个元素依次和后面的比较
int nowNumber = v[i];
// 计算出上个元素的索引
int backIndex = i - 1;
// 和上个元素以及之前的所有元素依次比较
while (backIndex >= 0 && nowNumber > v[backIndex]) {
// 元素往前移动
v[backIndex + 1] = v[backIndex];
backIndex -= 1;
}
// 最后找到了 要么 backIndex是-1 要么 backIndex位置的数值比 nowNumber 小
v[backIndex + 1] = nowNumber;
}
// 缩小间隔
s /= 2;
}
cout << v;
}
```
## 查找操作
### 二分查找
```
#include <iostream>
#include <vector>
using namespace std;
int search(const vector<int>& arr, int target) {
// 准备两个指针 代表 查找范围的索引区间
int l = 0, r = ((int) arr.size()) - 1;
// 开始进行迭代和循环 在循环中缩小区间
while (l <= r){
// 计算中间索引和中间数值
int midIndex = l + ((r - l) >> 1), midValue = arr[midIndex];
// 开始进行对比 决定要抛弃的区间
if (target < midValue) {
// 目标值比中间小,代表目标在左区间 舍弃右区间
r = midIndex - 1;
} else if (target > midValue){
// 目标值比中间大 代表目录在右区间 舍弃左区间
l = midIndex + 1;
} else {
// 这个情况代表 tar 和 基准值一样 找到索引了
return midIndex;
}
}
// 到这里代表没找到
return -1;
}
int main() {
vector<int> v{1, 2, 3, 4, 5, 6 ,7};
cout << search(v, 6) << endl;
cout << search(v, 4) << endl;
cout << search(v, 2) << endl;
cout << search(v, -2) << endl;
}
```
## 最优子结构
### 最大的顺序子序列之和
```
#include "iostream"
#include "vector"
using namespace std;
int maxSubArray(vector<int>& nums) {
// 当前最大子段和,初始化为第一个元素
int currentMax = nums[0];
// 全局最大子段和,也是第一个元素,目前是这样的
int maxSum = nums[0];
// 从第二个元素开始遍历
for (int i = 1; i < nums.size(); ++i) {
// 决定是否把当前元素加入前面的子段,还是重新开始一个子段
// 如果累加之后还没有当前元素大,那累加的结果就没必要了,也就说明要舍弃之前的记录,当前的元素单开一页,而不是加入之前的结果
// 如果加入的话 这个 currentMax 就会带着之前的累加结果继续加 nums[i]
currentMax = max(nums[i], currentMax + nums[i]);
// 更新全局最大值 每次计算出一个序列的最大值后,在这里都需要进行一个更新,及时将最大的结果得到
maxSum = max(maxSum, currentMax);
}
return maxSum;
}
int main() {
// 标记需要被计算的数组
// 要求计算出这个数组中最大的子序列(要求元素是连续的)之和
// 子序列就是这个数组的一部分的意思,比如 4 -1 2 -1 中 随意n个组合
// 顺序子序列就是组合的时候不调换顺序
auto v = vector<int>{-2, 1, -3, 4, -1, 2, 1, -5, 4};
cout << maxSubArray(v) << endl;
}
```
### 最大子数组乘积
```
#include "iostream"
#include "vector"
using namespace std;
int maxMArray(vector<int>& nums) {
// 首先初始化一个数值 代表 nums 中顺序子序列的最大乘积
int maxM = nums[0];
// 然后初始化一个存储器 用来记录一个子序列乘积的结果 用来累计计算
// TODO 还需要初始化一个数值 代表最小值,举个例子 很小很小的数值 -10000 如果乘-1 就变大了
int nowMaxM = nums[0], nowMinM = nums[0];
// 开始进行循环 这一步就是往 nowM 堆数值进行累乘,也就是序列追加数字,追加后 如果比记录的最大乘积
for (int i = 1; i < nums.size(); ++i) {
// 分别计算出最小值和最大值与当前值的乘积
int tempMax = nowMaxM * nums[i];
int tempMin = nowMinM * nums[i];
// 大小调换位置
if (tempMin > tempMax) {
int temp = tempMax;
tempMax = tempMin;
tempMin = temp;
}
// 更新当前的统计
nowMaxM = max(tempMax, nums[i]);
nowMinM = min(tempMin, nums[i]);
// 更新最大乘积
maxM = max(nowMaxM, maxM);
}
return maxM;
}
int main() {
// 标记需要被计算的数组
// 要求计算出这个数组中最大的子序列(要求元素是连续的)之乘积
// 子序列就是这个数组的一部分的意思,比如 4 -1 2 -1 中 随意n个组合
// 顺序子序列就是组合的时候不调换顺序
auto v = vector<int>{4, -1, 2, 1, -5, 4};
cout << maxMArray(v) << endl;
}
```
### 最大递增子序列
```
#include "iostream"
#include "vector"
using namespace std;
void operator <<(ostream& out, vector<int>& numbers) {
auto start = numbers.begin();
auto end = numbers.end();
while (start != end) {
out << *(start++) << ',';
}
out << endl;
}
// 最长连续递增子序列
vector<int> maxAddArray(vector<int>& nums) {
// 初始化一个数值 表示最终得到的最大连续递增的长度
int maxLen = 1;
int maxStartLen = 0;
// 初始化一个数值 表示当前连续递增的序列长度
int len = 1;
// 初始化一个数值 表示当前连续递增序列的开始索引
int startLen = 0;
for (int i = 1; i < nums.size(); ++i) {
// 当前元素和上一个比较 如果是递增就继续
if (nums[i] > nums[startLen + len - 1]) {
// 代表当前元素比上一个大 可以继续递增
len++;
} else {
// 代表需要单开一页了
if (maxLen < len) {
// 单开一页的时候一定要记得看一下 maxLen 是否真的最大
// 如果记录的 len 更大 则需要舍弃旧的记录 它破纪录了!
maxLen = len;
maxStartLen = startLen;
}
// 开始进行更新
startLen = i;
len = 1;
}
}
// 确定一下
// 构建出新的序列
vector<int> res(nums.begin() + maxStartLen, nums.begin() + maxStartLen + maxLen);
return res;
}
int main() {
// 找到这个数组中最长递增子序列
auto v = vector<int>{4, -1, 2, 1, 2, 3, 4, -5, 4};
auto res = maxAddArray(v);
cout << res;
delete &res;
}
```
# 贪心算法
贪心算法是一种在每一步选择中都采取当前状态下最好或最优(即最有利)的选择,从而希望导致结果是全局最优的算法。
## 硬币找零
🌰 举个例子:找零钱
面值:1, 5, 10, 50, 100
要找 37 元
贪心选择:先拿 100?不行 → 拿 50?不行 → 拿 10 → 可以!拿 3 个 10 元
然后拿 5 元,再拿 2 个 1 元
👉 虽然没考虑“未来”,但结果是最优的:6 枚硬币
✅ 这就是贪心选择性质:局部最优 → 全局最优
```
#include <vector>
#include <map>
#include "iostream"
using namespace std;
int main() {
system("chcp 65001");
// 小明去商店买一本书,书的价格是 price 元,他给了收银员 pay 元(pay >= price)。商店有以下几种面值的硬币:1元、5元、10元、50元、100元。
// 请问:收银员最少需要找给小明多少枚硬币?
// 可以选择的面值
auto cho = vector<int>{100, 50, 10, 5, 1};
// 计算出当前需要找的价格
int price = 15;
// 计算出支付的价格
int pay = 30;
// 计算出需要找的钱(注意 这个是剩余需要找的钱)
int remaining = pay - price;
cout << "应找金额 " << remaining << endl;
// 初始化一个 map 用于 key是面值,value是这个数量
auto m = map<int, int>();
// 开始进行调整 依次迭代 cho 的所有面值
for (const auto &item: cho) {
// 如果当前面值太大了 就跳过 这个不能找回去前
// 比如 小明给了10元 你不能找 100 回去
if (item < remaining) {
// 如果当前面值小 就计算一下看看需要多少个当前的钱
int count = remaining / item;
// count 就是我们记住的一个值 记录下来
m[item] = count;
// 然后个需要找的钱减去这一部分 因为这一部分已经找了
remaining -= (item * count);
}
}
// 打印出找钱的详情
for (const auto &item: m) {
cout << item.first << " 面值的硬币需要 " << item.second << endl;
}
// 这样是可以计算出需要的金额 但是为什么说是最少的硬币呢?
// 答案:cho 的顺序很关键,它正序迭代顺序,如果找到可以找的起的面值,这个面值一定是最大的,因为它是降序排序且是正序迭代!
// 为什么可以计算出数量呢?
// 答案 noPay / item 很重要,它就是计算出当前需要找的金额需要多少个 item 面值的金币
}
```
------
***操作记录***
作者:[zhao](https://www.lingyuzhao.top//index.html?search=4 "zhao")
操作时间:2025-08-05 20:00:28 星期二 【时区:UTC 8】
事件描述备注:保存/发布
中国 天津市 天津
[](如果不需要此记录可以手动删除,每次保存都会自动的追加记录)
